Beautiful Minds

Welcome back to Beautiful Minds of Math, everyone! Today’s entry will focus on Thomas Bayes. 

Your inbox dodges spam, and recommendation engines guess your next favorite song, all thanks to one elegant update rule from a soft-spoken thinker named Thomas Bayes. Let’s meet the mathematician and his theorem that teaches numbers to change their minds.

Thomas Bayes was an English theologian and Mathematician who lived in London in the 18th century. Although Bayes was nowhere near as much of a household name as other famous contemporary mathematicians were in his time, he was still a revolutionary. This may have been because Bayes was less of a pure mathematician and more of a statistician, but this by no means detracted from his accomplishments. 

If you asked a hundred mathematicians what Bayes’ greatest contribution to mathematics was, all one hundred of them would probably respond with Bayes’s theorem: a formula in probability theory that describes how to update the probability of a hypothesis based on new evidence, it allows you to reverse conditional probabilities, calculating the likelihood of a cause given its effect by relating it to the probability of the effect given the cause, the initial (prior) probability of the cause, and the overall probability of the evidence. 

A ubiquitous formula among students in the AP statistics course, Bayes’ theorem is used to solve problems that fall under the listed conditions above. Bayes’ insight is beautifully human: start with what you believe, then let new evidence nudge you, up or down, toward the truth. In practice, you carry a prior, weigh how likely the evidence would be if each explanation were true (the likelihood), and emerge with a sharper posterior (an upgraded belief). That’s why a “95% accurate” medical test isn’t a slam dunk when a disease is rare, and why your streaming app gets braver about recommending a weird indie film after you’ve loved three others. We can also turn this intuition into a compact equation and see how it flips questions like “How likely is this evidence if my idea is right?” into “How likely is my idea given this evidence?” 

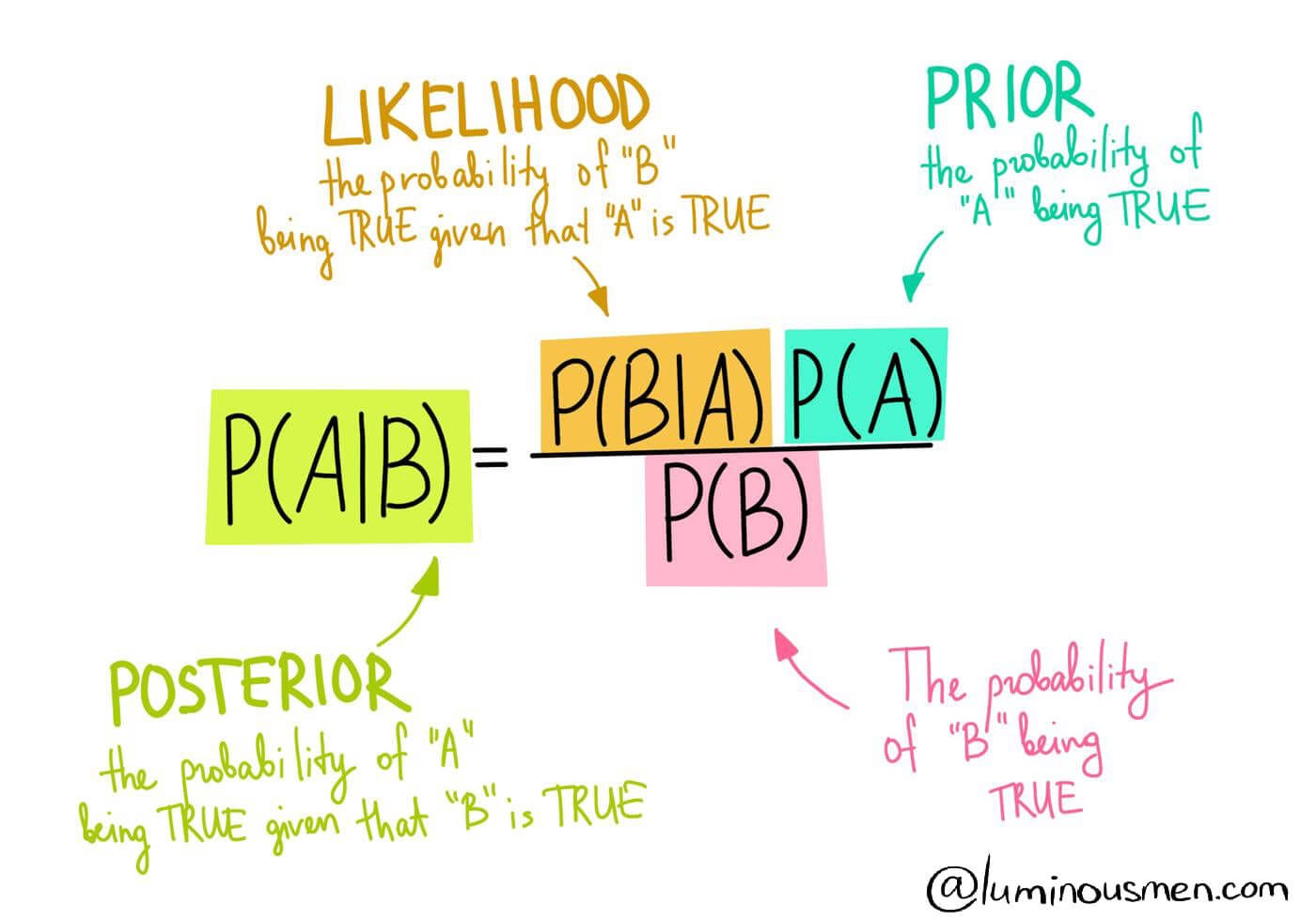
This theorem is denoted mathematically as such: P(H|E) = P(E|H) * P(H) / P(E). Here, H is the hypothesis and E is the evidence. P(H) is the prior, which is the belief in H before seeing E, P(E|H) is the likelihood (how expected E is if were true), P(E) is the marginal likelihood, denoting how common E is overall, and P(H|E) is the posterior (your updated belief after seeing E). If you have several mutually exclusive hypotheses, H of 1 all the way to some H of n, compute the denominator with the law of total probability. 

For modern statisticians, this theorem may not appear to be that crazy to conceive, as it is merely derived from the definition of conditional probability. However, it has greatly advanced the field of statistics and mathematics in general. Thomas Bayes (unfortunately) did not receive credit during his lifetime for Bayes’ theorem because he did not publish it himself; his friend Richard Price published the work in 1763 after recognizing its importance and finding applications for it. Additionally, the philosophy surrounding Bayesian thought was a source of contention: the theorem wasn’t widely adopted until its importance was later recognized by others like Pierre Simon Laplace and eventually the wider scientific community in the 20th century. 

“Under Bayes’ theorem, no theory is perfect. Rather, it is a work in progress, always subject to further refinement and testing.” – Nate Silver, an American statistician

Works Cited: 

Dasadiya, Vishvdeep. “What Is the Bayes’ Theorem?” Medium, 22 Nov. 2021, aiwithvd.medium.com/what-is-the-bayes-theorem-545a2ef0b91c. Accessed 7 Oct. 2025.

Khan Academy. “Check Independence: Conditional Probability.” Khan Academy, https://www.khanacademy.org/math/ap-statistics/probability-ap/stats-conditional-probability/a/check-independence-conditional-probability. Accessed 7 Oct. 2025.

Siegmund, David O. “Applications of Conditional Probability.” Encyclopaedia Britannica, 5 Sept. 2025, https://www.britannica.com/science/probability-theory/Applications-of-conditional-probability. Accessed 7 Oct. 2025.

“The Editors of Encyclopaedia Britannica.” “Thomas Bayes.” Encyclopaedia Britannica, https://www.britannica.com/biography/Thomas-Bayes. Accessed 7 Oct. 2025.