Beautiful Minds

Have you ever heard of a problem so absurd that a 5th grader can understand it, but not even the finest mathematical minds in the world can solve it? Introducing the Collatz Conjecture. 

The Collatz conjecture is a famous problem in mathematics proposed by German mathematician Lothar Collatz in 1937. Collatz was a student at the University of Hamburg when he introduced the problem in a seminar and included it in the margin of his diary. He shared the problem informally with colleagues but did not publish it himself, so it became known through word of mouth among mathematicians. Because Collatz never published a formal paper on it, the conjecture has been independently rediscovered multiple times and is known by various names, including the 3n+1 problem, the Syracuse problem, and Kakutani’s problem. 

Lothar Collatz’s introduction of the problem was almost accidental. He had a habit of exploring small processes, often jotting down ideas in the margins of notebooks. One of these happened to be an intriguing problem he couldn’t solve in his studies: the infamous Collatz Conjecture. He brought this sudden idea up casually during seminars, and because he never published it formally, the problem escaped into mathematical circles rapidly. This informal spread is why the conjecture keeps being rediscovered independently and has been associated with several other different names.

3n+1. That is it. That is the Collatz Conjecture in its entirety. 

Well, almost. You see, the Collatz conjecture is, in theory, very simple and could probably be understood by even a 5th grader: pick any number to begin with, then multiply it by 3 and add 1 to it if the initial number is odd, and divide it by 2 if the initial number is even, and repeat this process constantly.

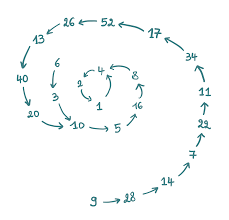
Let’s try it with a random number: if we take the number 17, we would get: 

17×3+1 = 52

52/2 = 26

 26/2 = 13

13×3+1 = 40

 40/2 = 20

20/2 = 10

10/2 = 5

5×3+1 = 16

16/2 = 82

8/2 = 4

4/2 = 2

2/2 = 1

1×3+1 = 4

4/2 = 2

2/2 = 1

After several rounds of applying the rules and calculations, we end up at an infinitely repeating loop of 4-2-1. Coincidence? I think not. Actually, this fascinating pattern applies to essentially any number that you select (and it has for the vast set of numbers that have been tested by mathematicians and computer algorithms). But why does this happen? Why does a seemingly random mathematical algorithm applied to any arbitrary number lead to this result? 

The “conjecture” part of the problem is derived from the statement that for any positive integer selected, this pattern of eventually coming down to the 4-2-1 cycle will hold. In fact, the conjecture has been shown to hold for all positive integers up to 2.36×10^21, but no general proof has been found that would show this pattern would extend to all positive integers. 

Despite the simplicity of the rule, proving the Collatz Conjecture has turned out to be exceptionally difficult. One major reason is the unpredictable nature of the sequences it produces. While every tested number eventually falls into the 4-2-1 cycle, the path it takes to get there can be wildly erratic. Some numbers decrease quickly, while others balloon to enormous heights before collapsing; there is no known formula or structure that allows mathematicians to predict these behaviors in general. Each step of the sequence can drastically change the number, and because the rule intertwines multiplication, addition, and division, the resulting behavior resembles chaotic dynamical systems more than traditional number theory. Therefore, graph and tree theory have been used to try to map these paths. In essence, the conjecture is hard to prove because it is governed by extremely simple rules that nonetheless give rise to patterns too complex for current mathematical tools to tame.

The structure generated by the Collatz rules also has interesting connections to cryptography. Though the conjecture itself is not used directly, the behavior of the function resembles the kind of unpredictable, chaotic transformations that are valuable in cryptographic systems. The repeated application of a simple rule that produces outputs that appear pseudo-random makes Collatz-style maps compelling candidates for pseudorandom number generators and hashing functions. Furthermore, the difficulty of inverting the Collatz step, since many different numbers can map to the same output, and the rule mixes operations unpredictably, resembles the structure of one-way functions in cryptography. Thus, while the conjecture remains unsolved, its behavior provides insight into computational unpredictability, an idea central to modern cryptography.

Collatz’s achievements and contributions to the math world extended far beyond the Collatz Conjecture: he was the author of several other publications, such as one where he showed a more efficient way to approximate the complex solutions of an algebraic equation. In another publication, Collatz introduced ways to solve certain differential equations and their practical applications as well. Despite all of his brilliance, he remained humble. According to two German mathematicians, Meinardus and Nürnberger, “Professor Collatz was a truly wonderful individual. He was modest in his behavior and ever amiable and helpful.” Collatz passed away in Bulgaria, where he was to attend a math conference on computer arithmetic (fittingly). Although Collatz has unfortunately passed away, his contributions and tricky conjecture live on and continue to stump young mathematicians to this very day. 

Bibliography

Hemelaer, Jens. “The Collatz Topos.” Jens Hemelaer, 26 July 2023, jenshemelaer.com/2023/07/26/collatz-topos.html.

“Lothar Collatz (1910–1990).” MacTutor History of Mathematics Archive, University of St Andrews, Nov. 2006, mathshistory.st-andrews.ac.uk/Biographies/Collatz/.

Orús-Lacort, Mercedes, and Christophe Jouis. “Analyzing the Collatz Conjecture Using the Mathematical Complete Induction Method.” Mathematics, vol. 10, no. 12, 2022, p. 1972. MDPI, https://doi.org/10.3390/math10121972.

“The Collatz Conjecture.” Art of Problem Solving, 2014, artofproblemsolving.com/community/c1507h1000417_collatz_conjecture.